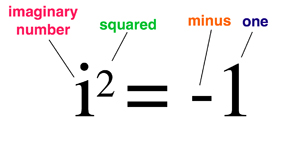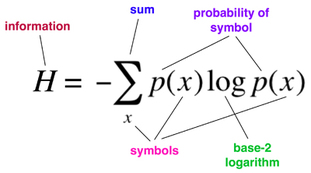17 Equations That Changed the World
To avoide the tediouse repetition of these woordes: is equalle to:
I will sette as I doe often in woorke use, a paire of paralleles,
or gemowe lines of one lengthe: ========== , bicause
noe .2. thynges, can be moare equalle.
Robert Recorde, The Whetstone of Witte, 1557
I will sette as I doe often in woorke use, a paire of paralleles,
or gemowe lines of one lengthe: ========== , bicause
noe .2. thynges, can be moare equalle.
Robert Recorde, The Whetstone of Witte, 1557
|
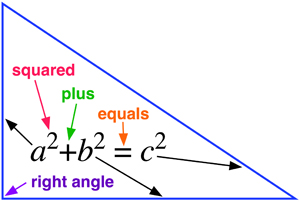
Pythagoras
What does it tell us? How the three sides of a right-angled triangle are related. Why is that important? It provides a vital link between geometry and algebra, allowing us to calculate distances in terms of coordinates. It also inspired trigonometry. What did it lead to? Surveying, navigation, and more recently special and general relativity—the best current theories of space, time, and gravity. |
|
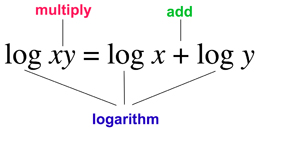
Logarithms
What does it tell us? How to multiply numbers by adding related numbers instead. Why is that important? Addition is much simpler than multiplication. What did it lead to? Efficient methods for calculating astronomical phenomena such as eclipses and planetary orbits. Quick ways to perform scientific calculations. The engineers’ faithful companion, the slide rule. Radioactive decay and the psychophysics of human perception. |
|
Calculus
What does it say? To find the instantaneous rate of change of a quantity that varies with (say) time, calculate how its value changes over a short time interval and divide by the time concerned. Then let that interval become arbitrarily small. Why is that important? It provides a rigorous basis for calculus, the main way scientists model the natural world. What did it lead to? Calculation of tangents and areas. Formulas for volumes of solids and lengths of curves. Newton’s Laws of Motion, differential equations. The Laws of Conservation of Energy and Momentum. Most of mathematical physics. |
|
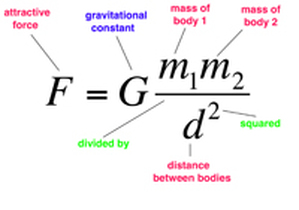
Newton's Law of Gravity
What does it say? It determines the force of gravitational attraction between two bodies in terms of their masses and the distance between them. Why is that important? It can be applied to any system of bodies interacting through the force of gravity, such as the solar system. It tells us that their motion is determined by a simple mathematical law. What did it lead to? Accurate prediction of eclipses, planetary orbits, the return of comets, the rotation of galaxies. Artificial satellites, surveys of the Earth, the Hubble telescope, observations of solar flares. Interplanetary probes, Mars rovers, satellite communications and television, the Global Positioning System. |
|
Complex Numbers
What does it say? Even though it ought to be impossible, the square of the number i is minus one. Why is that important? It led to the creation of complex numbers, which in turn led to complex analysis, one of the most powerful areas of mathematics. What did it lead to? Improved methods to calculate trigonometric tables. Generalisations of almost all mathematics to the complex realm. More powerful methods to understand waves, heat, electricity, and magnetism. The mathematical basis of quantum mechanics. |
|
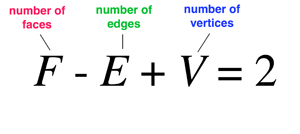
Euler's Formula for Polyhedra
What does it say? The numbers of faces, edges, and vertices of a solid are not independent, but are related in a simple manner. Why is that important? It distinguishes between solids with different topologies using the earliest example of a topological invariant. This paved the way to more general and more powerful techniques, creating a new branch of mathematics. What did it lead to? One of the most important and powerful areas of pure mathematics: topology, which studies geometric properties that are unchanged by continuous deformations. Examples include surfaces, knots, and links. Most applications are indirect, but its influence behind the scenes is vital. It helps us understand how enzymes act on DNA in a cell, and why the motion of celestial bodies can be chaotic. |
|
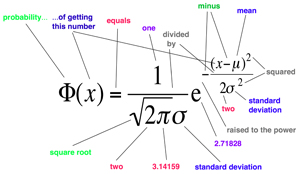
Normal Distribution
What does it say? The probability of observing a particular data value is greatest near the mean value—the average—and dies away rapidly as the difference from the mean increases. How rapidly depends on the standard deviation. Why is that important? It defines a special family of bell-shaped probability distributions, which are often good models of common real-world observations. What did it lead to? The concept of the ‘average man’, tests of the significance of experimental results, such as medical trials, and an unfortunate tendency to default to the bell curve as if nothing else existed. |
|
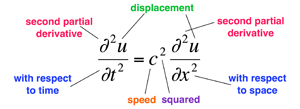
Wave Equation
What does it say? The acceleration of a small segment of a violin string is proportional to the average displacement of neighbouring segments. Why is that important? It predicts that the string will move in waves, and it generalises naturally to other physical systems in which waves occur. What did it lead to? Big advances in our understanding of water waves, sound waves, light waves, elastic vibrations... Seismologists use modified versions of it to deduce the structure of the interior of the Earth from how it vibrates. Oil companies use similar methods to find oil. In Chapter 11 we will see how it predicted the existence of electromagnetic waves, leading to radio, television, radar, and modern communications. |
|
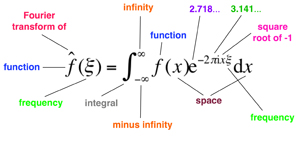
Fourier Transform
What does it say? Any pattern in space and time can be thought of as a superposition of sinusoidal patterns with different frequencies. Why is that important? The component frequencies can be used to analyse the patterns, create them to order, extract important features, and remove random noise. What did it lead to? Image processing and quantum mechanics. Structure of large biological molecules like DNA. Image compression in digital photography, cleaning up old or damaged audio recordings, analysing earthquakes. Modern variants are used to store fingerprint data efficiently and improve medical scanners. |
|
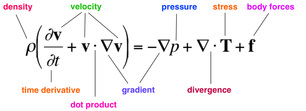
Navier-Stokes
What does it say? It’s Newton’s Second Law of Motion in disguise. The left-hand side is the acceleration of a small region of fluid. The right-hand side is the forces that act on it: pressure, stress, and internal body forces. Why is that important? It provides a really accurate way to calculate how fluids move. This is a key feature of innumerable scientific and technological problems. What did it lead to? Modern passenger jets, fast and quiet submarines, Formula-1 racing cars that stay on the track at high speeds, and medical advances on blood flow in veins and arteries. Computer methods for solving the equations, known as Computational Fluid Dynamics (CFD), are widely used by engineers to improve technology in such areas. |
|
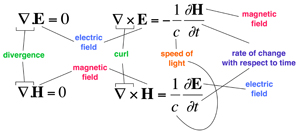
Maxwell's Equations
What do they say? Electricity and magnetism can’t just leak away. A spinning region of electric field creates a magnetic field at right angles to the spin. A spinning region of magnetic field creates an electric field at right angles to the spin, but in the opposite direction. Why is that important? It was the first major unification of physical forces, showing that electricity and magnetism are intimately interrelated. What did it lead to? The prediction that electromagnetic waves exist, travelling at the speed of light, so light itself is such a wave. This motivated the invention of radio, radar, television, wireless connections for computer equipment, and most modern communications. |
|
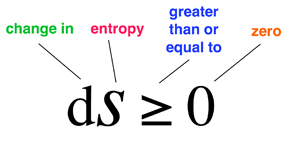
Second Law of Thermodynamics
What does it say? The amount of disorder in a thermodynamic system always increases. Why is that important? It places limits on how much useful work can be extracted from heat. What did it lead to? Better steam engines, estimates of the efficiency of renewable energy, the ‘heat death of the universe’ scenario, proof that matter is made of atoms, and paradoxical connections with the arrow of time. |
|
Relativity
What does it say? Matter contains energy equal to its mass multiplied by the square of the speed of light. Why is that important? The speed of light is huge and its square is absolutely humongous. One kilogramme of matter would release about 40% of the energy in the largest nuclear weapon ever exploded. It’s part of a package of equations that changed our view of space, time, matter, and gravity. What did it lead to? Radical new physics, definitely. Nuclear weapons... well, just maybe—though not as directly or conclusively as the urban myths claim. Black holes, the Big Bang, GPS and SatNav. |
|
Schrödinger Equation
What does it say? The equation models matter not as a particle, but as a wave, and describes how such a wave propagates. Why is that important? Schrödinger’s Equation is fundamental to quantum mechanics, which together with general relativity constitute today’s most effective theories of the physical universe. What did it lead to? A radical revision of physics at very small scales, in which every object has a ‘wave function’ that describes a probability cloud of possible states. At this level the world is inherently uncertain. Attempts to relate the microscopic quantum world to our macroscopic classical world led to philosophical issues that still reverberate. But experimentally, quantum theory works beautifully, and today’s computer chips and lasers wouldn’t work without it. |
|
Information Theory
What does it say? It defines how much information a message contains, in terms of the probabilities with which the symbols that make it up are likely to occur. Why is that important? It ushered in the Age of Information. It established limits on the efficiency of communications, allowing engineers to stop looking for codes that were too effective to exist. It is basic to today’s digital communications—phones, CDs, DVDs, the Internet. What did it lead to? Efficient error-detecting and error-correcting codes, used in everything from CDs to space probes. Applications include statistics, artificial intelligence, cryptography, and extracting meaning from DNA sequences. |
|
Chaos
What does it say? It models how a population of living creatures changes from one generation to the next, when there are limits to the available resources. Why is that important? It is one of the simplest equations that can generate deterministic chaos—apparently random behaviour with no random cause. What did it lead to? The realisation that simple nonlinear equations can create very complex dynamics, and that apparent randomness may conceal hidden order. Popularly known as Chaos Theory, this discovery has innumerable applications including the motion of the planets in the solar system, weather forecasting, population dynamics in ecology, variable stars, earthquake modelling, and efficient trajectories for space probes. |
|
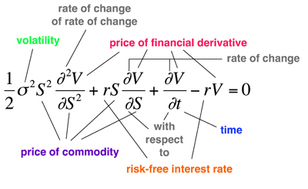
Black-Scholes Equation
What does it say? How the price of a financial derivative changes over time, based on the principle that when the price is correct, the derivative carries no risk and no one can make a profit by selling it at a different price. Why is that important? You can trade a derivative before it matures by assigning an agreed ‘rational’ value to it, so that it becomes a virtual commodity in its own right. What did it lead to? Massive growth of the financial sector, ever more complex financial instruments, surges in economic prosperity punctuated by crashes, the turbulent stock markets of the 1990s, the 2008-9 financial crisis, and the ongoing economic slump. |