THE GRAND UNIFICATION OF THE THEORY OF SPECIAL, GENERAL, AND TOTALLY INDISCRIMATE RELATIVISM, AND THE EXISTENCE OF TWIDARK
|
Big Al Onestone postulated that nothing can travel faster than light. Otherwise time and space get mixed up so much that you can receive a message before you send it.
This theory was widely accepted, until some annoying person pointed out that dark travels faster than light. That is, d > c. Undaunted, Onestone introduced a slight modification into his equations. He asserted that d is negative, but we are measuring it in the wrong direction. Dark does not move away from light at speed d. It moves towards light at speed –d. Now –d < c and all is well. Also ED = -m(-d)^2 = -md^2 is unchanged. |
TWIDARK ENERGY
The total energy is
EL + ED = mc^2 – md^2 < 0
which is paradoxical.
Physicists have decided that there must exist twidark energy ET to account for the discrepancy, so that
EL + ED + ET = 0
A formula known as Asymptotic Flatness of the Turtle. It follows that
ET = md^2 – mc^2
Bearing in mind that the speed of twidark is b, it seems reasonable to set
ET = mb^2
And the reader can easily verify that
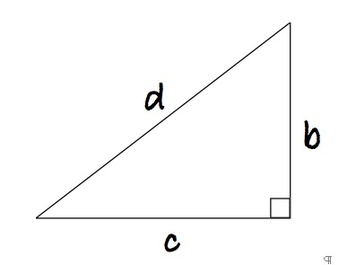
b^2 = d^2 – c^2
which we rewrite as
b^2 + c^2 = d^2
and recognise as Pthagonal’s Theorem (in non-standard notation). QED.
The total energy is
EL + ED = mc^2 – md^2 < 0
which is paradoxical.
Physicists have decided that there must exist twidark energy ET to account for the discrepancy, so that
EL + ED + ET = 0
A formula known as Asymptotic Flatness of the Turtle. It follows that
ET = md^2 – mc^2
Bearing in mind that the speed of twidark is b, it seems reasonable to set
ET = mb^2
And the reader can easily verify that
b^2 = d^2 – c^2
which we rewrite as
b^2 + c^2 = d^2
and recognise as Pthagonal’s Theorem (in non-standard notation). QED.
Solving for b we obtain
b = ±√(d^2 – c^2)
implying that twidark moves at a speed of either
+√(d^2 – c^2)
or
−√(d^2 – c^2)
Physicists feel that this dual-speed property must be important: it should allow twidark to join up properly with both light, which has positive speed, and dark, which has negative speed. However, neither answer agrees with our previous hypotheses☛, so the detailed calculations are elusive.
For example, if we average to two speeds we get b=0, which is one of our previous suggestions.
Alternatively, the average of the speeds of light and dark is
(c-d)/2
or, if you dispute Onestone’s ‘negative d’ proposal,
(c+d)/2
Compromising by taking the geometric mean we get
b^2 = (c-d)(c+d)/4
so
b = ±√(c^2-d^2)/2
which is exactly the same as we computed above.*
b = ±√(d^2 – c^2)
implying that twidark moves at a speed of either
+√(d^2 – c^2)
or
−√(d^2 – c^2)
Physicists feel that this dual-speed property must be important: it should allow twidark to join up properly with both light, which has positive speed, and dark, which has negative speed. However, neither answer agrees with our previous hypotheses☛, so the detailed calculations are elusive.
For example, if we average to two speeds we get b=0, which is one of our previous suggestions.
Alternatively, the average of the speeds of light and dark is
(c-d)/2
or, if you dispute Onestone’s ‘negative d’ proposal,
(c+d)/2
Compromising by taking the geometric mean we get
b^2 = (c-d)(c+d)/4
so
b = ±√(c^2-d^2)/2
which is exactly the same as we computed above.*
☛ Except ‘umpty’, for a given value of umpty.
* Well, actually it should be d^2-c^2 and the /2 is wrong as well, but this is cosmology. Anyway, if we divide by √-1/2 then we get exactly the same result. The number √-1/2 is called Plonk’s constant, because you can plonk it down wherever you need to make the calculation work out OK.
* Well, actually it should be d^2-c^2 and the /2 is wrong as well, but this is cosmology. Anyway, if we divide by √-1/2 then we get exactly the same result. The number √-1/2 is called Plonk’s constant, because you can plonk it down wherever you need to make the calculation work out OK.