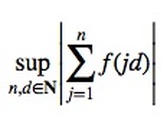What's Happening in Mathematics?
page 1 (oldest)
An occasionally updated series of links to mathematical news — new applications,
new discoveries, problems, personalities, prizes...
new discoveries, problems, personalities, prizes...
|
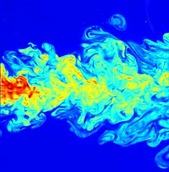
Important breakthrough by Dwight Barkley and others on the longstanding problem of the onset of turbulence for fluid flow in a pipe. Turbulence sets in as a localised burst, which travels much like a forest fire. A reaction-diffusion model reproduces bifurcation diagrams observed in real flows.
|
|
Terry Tao posts on the ArXiv a solution to the Erdös Discrepancy Problem: any infinite sequence of +1s and −1s has an equally spaced subsequence with an arbitrarily large (positive or negative) sum. Experts are confident the proof is correct, but it is currently under review. The method was suggested by a comment posted on Tao's blog.
|
|
New York Times interview with
Terry Tao, one of the world's top mathematicians. |
Includes Charlie Fefferman's brilliant description of mathematical research: like ‘‘playing chess with the Devil.’’ The Devil is vastly superior at chess, but you may take back as many moves as you like, and the Devil may not. You don't often win, but all you can lose is time.
|
|
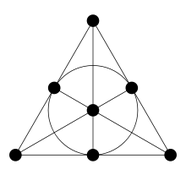
Surprising new results on 'designs', generalisations of the 150-year old Kirkman's schoolgirls problem. Given n objects, find a list of subsets of size k so that every set of size t appears in just one subset. In 2014 Peter Keevash proved that a standard necessary condition is almost always sufficient. Now he can count approximately how many (n,k,t) designs exist.
|
|
Mathematician Colin Wright organizes these events on a regular basis. They are an informal two-day event with maths-related themes. Almost anything can happen. He says:
"Anyone can join the fun. We have people of all ages, backgrounds, education and ability. All you need is an interest in and enthusiasm for maths of all types." |
|
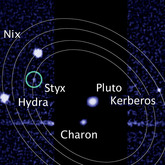
Astronomers believe the moons of Pluto are tumbling chaotically. This observation by the Hubble telescope will shortly be tested when New Horizons gets closer to the dwarf planet. Saturn's moon Hyperion is known to exhibit chaotic tumbling, which is potentially possible for any body with unequal axes of inertia.
|
|
John Nash, a mathematician who won the Nobel Prize in Economics for his research into game theory, is best known to the public through the book and movie A Beautiful Mind. On 23 May Nash and his wife Alicia died together in a taxi accident, while returning from Nash's award of the Abel Prize in Norway (see below)
|
|
Realistic CFD analysis of five scenarios for an airliner plunging into the ocean, with special reference to Malaysia Airlines MH370. Suggests the aircraft probably entered at a steep angle, which is why no floating debris was found. Includes link to video animations.
|
|
Brief comments on the viral puzzle and some questions it raises about public attitudes to mathematics and logical thinking.
For the answer, see Laura Bradley and Anne-Marie Lindemann's video solution or Alex Bellos's video solution. But why not have a go yourself first? Work through the conversation step by step and see which dates can be eliminated. |
|
New math magazine, free online, making the subject accessible, interesting, and entertaining. Created by mathematicians at UCL. Issue 01 has everything from a mathematicians' haircuts top ten to wormholes. Issue 2 is now in print.
|
|
The 2015 Abel prize winners are John Nash and Louis Nirenberg, “for striking and seminal contributions to the theory of nonlinear partial differential equations and its applications to geometric analysis.”
|
|
Manjul Bhargava and Arul Shankar. Ternary cubic forms having bounded invariants, and the existence of a positive proportion of elliptic curves having rank 0, Annals of Math. 181 (2015) 587-621. Publication of 2010 arXiv article proving that a nonzero proportion of elliptic curves have rank 0 and 1. Implies the Millennium Prize Birch—Swinnerton-Dyer Conjecture is true for a nonzero proportion of elliptic curves.
|
|
The triangulation conjecture: every manifold can be cut into simplexes (analogues of triangles in any dimension). By 1950 this conjecture had been proved true for manifolds of dimensions 1,2, 3; in the 1980s Andrew Casson showed that it is false in dimension 4. However, it remained plausible that the triangulation conjecture is true in all dimensions except 4. No longer. Ciprian Manolescu has posted online a proof that it is false in all dimensions greater than or equal to 4.
|
|
What comes after Perelman's proof of the Poincaré Conjecture and the Geometrization Theorem. States that a compact orientable irreducible 3-manifold with infinite fundamental group is virtually Haken — it has a finite cover that is a Haken manifold. Ian Agol announced a proof in March 2012. It is now on the ArXiv.
|