What's Happening in Mathematics?
page 4
An occasionally updated series of links to mathematical news — new applications,
new discoveries, problems, personalities, prizes...
new discoveries, problems, personalities, prizes...
|
An AI program from Google's DeepMind has taught itself how to play Go better than any human, in three days, starting only from the rules of the game. Previous Go algorithms used more than 100,000 human games played by experts. The new algorithm plays random moves against itself and learns what works best. It is based on the mathematical technique of Deep Learning, in which connection strengths an artificial neural network are updated according to experience.
|
|
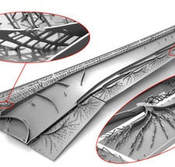
Niels Aage, Erik Andreassen, Boyan S. Lazarov and Ole Sigmund apply topology optimization, a computer-aided method, to design the internal structure of an aeroplane wing. The design has unprecedented structural detail at length scales ranging from tens of metres to millimetres and shows remarkable similarity to natural bone structures in bird beaks. The method enables unrestricted design freedom and shows great promise with regard to weight savings.
|
|
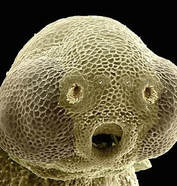
How do fish sense the flow of a surrounding fluid when they are swimming in it? Pablo Oteiza and colleagues provide evidence that zebrafish larvae use the lateral line of nerve cells to convert a line integral of the flow field to an area integral of the local vorticity — in effect, a biological exploitation of Stokes' Theorem in vector calculus.
|
|
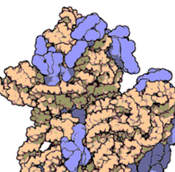
The ribosome is a complex molecular machine that performs protein synthesis in cells. Ribosomes join amino acids together in the order specified by messenger RNA. Shlomi Reuveni, Måns Ehrenberg and Johan Paulsson show mathematically that many features of ribosomes — such as why a few ribosomal RNA molecules dominate the mass and why ribosomal proteins are divided into 55–80 small, similarly sized segments — optimise their autocatalytic production.
|
|
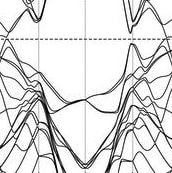
Barry Bradlyn and coauthors use mathematical tools to predict large numbers of new topological insulators and semimetals. Their electronic band theory links topology and chemical bonding to describe band structures and materials. Using graph theory to describe momentum space and group theory to describe real space, they classify all possible band structures for the 230 crystal symmetry groups, and find the topologically
non-trivial ones. |
|
The Kepler Conjecture states that the closest sphere-packing in space is the face centred cubic lattice — essentially, how greengrocers stack oranges, extended to infinity. The 1998 proof by Thomas Hales involved extensive computer calculations, and the referees were unable to verify them. Now a team headed by Hales has published a proof in a strict logical form that can be, and has been, verified by computer.
|
|
Maryam Mirzakhani, the first woman to be awarded the prestigious Fields Medal for mathematics, has died aged 40. She made important breakthroughs in dynamics and the geometry of Riemann surfaces and their moduli spaces.
|
|
Liana Manukyan and coworkers show that the patterns formed by the scales of ocellated lizards are a very close match to a model by Turing reaction-diffusion equations, discretized to become a continuous-state cellular automation model on a hexagonal (or approximately so) lattice. The model can also be viewed as a coupled cell ODE on a network.
|
|
The Norwegian Academy of Science and Letters has awarded the Abel Prize for 2017 to Yves Meyer of the École normale supérieure Paris-Saclay, France “for his pivotal role in the development of the mathematical theory of wavelets”. Wavelet analysis has been applied to data compression, noise reduction, medical imaging, digital cinema, the Hubble space telescope, and LIGO's detection of gravitational waves caused by two colliding black holes.
|
|
In 2014 Thomas Royen, a retired German statistician, was brushing his teeth when he realised how to prove the long-sought Gaussian Correlation Inequality, conjectured in 1955. For a variety of reasons his proof went unnoticed until a few months ago, but it has now received proper recognition. The inequality states that if μ is n-dimensional Gaussian measure, then for all convex sets E , F in n-dimensional space that are symmetric about the origin, the inequality
μ(E∩F) ≥ μ(E) μ(F) holds. |
|
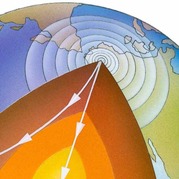
Plamen Stefanov, Gunther Uhlmann, and Andras Vasy have proved the boundary-rigidity conjecture for Riemannian manifolds — knowing the distance along geodesics between any two points on the boundary determines the metric (under suitable hypotheses). The 2-dimensional case was proved in 2005; the new proof is general. There is an important application to seismology: the internal structure of the Earth can be inferred from travel times of seismic waves between any two points on the surface.
|
|
London's Science Museum has opened its new Winton Gallery, dedicated to mathematics and designed by architect Zaha Hadid.
|
|
Hydrant in Berlin
|
Images of numbers from all over Europe... and tomorrow, the world! Numbers on doors, numbers on walls... Numbers! Is your home town represented? If not, take a photo and send one in.
|
|
In 2012 the Japanese mathematician Shinichi Mochizuki published a 500-page proof, online, of the ABC conjecture. This is one of the most important unsolved problems in number theory, and a correct proof would be revolutionary. Optimism is now growing that the proof is right. The conjecture relates the prime factors of three numbers a, b, c such that a + b = c. This looks very simple, but the consequences of the relationship are deep and powerful.
|
|
Marijn J. H. Heule, Oliver Kullmann, and Victor W. Marek have announced that it is impossible to colour the positive integers with two colours so that every Pythagorean triple uses both colours. They show this can be done for integers up to 7,824, but fails when 7,825 is included. The proof, intelligent case-by-case checking, occupies 200 terabytes — a record.
|
|
John Cremona at the University of Warwick is the lead UK researcher on a 12-nation database of mathematical objects that has been deployed to protect bank accounts and solve problems in physics and prime number theory. The team has catalogued over a billion mathematical items including elliptic curves, modular forms, L-functions, and non-trivial zeros, in the research initiative L-Functions and Modular Forms Database Project at: http://www.lmfdb.org/
|