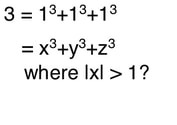What's Happening in Mathematics?
page 6 (newest)
An occasionally updated series of links to mathematical news — new applications,
new discoveries, problems, personalities, prizes...
new discoveries, problems, personalities, prizes...
|
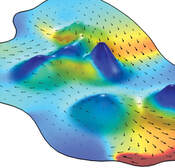
The collective behavior of active agents is a hot area in biological and soft matter physics. Christina Hueschen, Alexander Dunn, and Rob Phillips apply Toner-Tu flocking theory to describe the movement of a herd of wildebeest in hilly terrain.
|
|
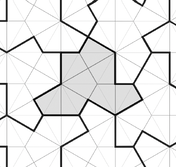
The recently discovered “hat” aperiodic monotile mixes unreflected and reflected
tiles in every tiling it admits. David Smith, Joseph Samuel Myers, Craig S. Kaplan, and Chaim Goodman-Strauss show that a close relative of the hat admits only non-periodic tilings if we forbid reflections. Modifying this polygon’s edges gives a family of shapes called spectres that are admit only chiral non-periodic tilings. |
|
Sets of tiles that can tile the plane, but not in any periodic lattice pattern, have long been known. Roger Penrose found such a set with just two tiles, but it has been open whether a single tile can do the trick. David Smith, Joseph Samuel Myers, Craig S. Kaplan, and Chaim Goodman-Strauss have now found such a tile.
|
|
In how many ways can n queens be placed on an nxn chessboard so that they do not attack each other? there are 92 different configurations when n = 8, the usual chessboard. Now Michael Simkin has proved that when n is large there are approximately (0.143n)^n configurations. The proof sandwiches the exact number between two bounds, both close together, using sophisticated methods.
|
|
Squaring the circle using ruler and compasses is known to be impossible. In 1990 Miklós Laczkovich showed that a circle can be dissected into finitely many pieces that reassemnble to form a square. (The pieces are complicated and disconnected, unlike a conventional jigsaw.) Andras Máthé, Oleg Pikhurko, and Jonathan Noel have improved his construction. They need about 10^200 pieces, but they're simpler. Conjecturally, 22 will do the job.
|
|
Joshua Evan Greene and Andrew Lobb have proved that for every smooth Jordan curve K and rectangle R in the Euclidean plane, there exists a rectangle similar to R whose vertices lie on K. The proof relies on Shevchishin's theorem that the Klein bottle does not admit a smooth Lagrangian embedding in ℂ^2.
|
|
Before electronic computers there were mechanical ones, from the Antikythera machine to hand-cranked calculators. Mechanical computation is now witnessing a revival, in which adaptable materials and structures form a distributed information processing network, so that information processing can be viewed as a material property. Hiromi Yasuda and others survey the area.
|
|
Knot theory has now become important in areas of science from biology to quantum physics. Kai Wang, Avik Dutt, Charles Wojcik and Shanhui Fan describe theory and experiments connecting the braid group B2 to non-Hermitian periodic systems, where topological properties lead to robust quantum and classical systems. They observe a wide variety of two-band braiding structures that include the unlink, unknot, Hopf link, and trefoil. Similar methods should apply to all braid groups Bn.
|
|
The rational points on an elliptic curve form a finitely generated abelian group, so it has finite rank. The largest known rank is 28, but it is widely believed that the ranks are unbounded. Jennifer Park, Bjorn Poonen, John Voight, Melanie Matchett Wood have published a preprint in the ArXiv using random matrix theory to argue heuristically that only finitely many elliptic curves have rank greater than 21.
|
|
Swiss researchers have calculated pi to 62.8
trillion decimal places using a supercomputer.
The calculation took 108 days, and beats the previous world-record of 50 trillion decimal places.
|
|
What shape is an egg? Until now, the huge variety of egg shapes has defeated all attempt to find a universal formula: one that generates all known shapes when parameters are set to suitable values. Now a team led by Darren Griffin,at the University of Kent has cracked this longstanding problem.
|
|
Ido Kaminer and colleagues at the Technion have developed the Ramanujan Machine: an algorithm that creates plausible mathematical conjectures, which challenges mathematicians to prove them. The formulas are continued fraction expansions of interesting numbers. One discovery is a new algebraic structure related to Catalan's constant. The self-taught genius Srinivasa Ramanujan was famous for finding formulas of this kind — and many others.
|
|
Which numbers n can be written as a sum of three integer cubes, and how? Recently Drew Sutherland and Andy Booker found how to do this for the only number between 1 and 100 for which the answer was unknown: n=42. Now they've found a solution for n=3. Obviously 3 = 13+13+13 — but what's the next solution, if any?
They found it: 569936821221962380720^3 + (-569936821113563493509)^3 + (-472715493453327032)^3 = 3. |
|
Obituary by Georgina Ferry in The Guardian
|
Bob May was a pioneer of chaos theory, applying it to population dynamics of animals. His no-nonsense attitude was refreshing and unusual. He was President of the Royal Society and Chief Scientific Adviser to the government. He also used ecological modelling principles to suggest improvements to the banking system and mathematical economics after the financial crash of 2008.
|
|
Obituary by Colm Mulcahy in The Guardian
|
One of the world's most loved, and eccentric, mathematicians has died of COVID-19. Conway was always inventive, amusing, a brilliant lecturer, with an impressive ability to work with complicated combinatorial structures. His legacy includes the Game of Life, the three Conway simple groups, the Monster simple group, monstrous moonshine, surreal numbers, lattices, and a comprehensive theory of mathematical games. And much, much more.
|
|
Antonino Morassi and Alexandre Kawano present a theoretical mechanical model of how an orb-web spider works out where its prey has hit its web, from how the web vibrates. This is an 'inverse problem of source identification'. They use a continuous membrane model to represent the web's structural connectivity. Their equations
help identify the key parameters for the web's response — hence also the spider's. |
|
A giant leap for bivalve-kind
|
Alain Goriely and Régis Chirat (U Oxford) explain the interlocking mechanism of bivalve shells using a mathematical model of shell growth, especially the geometry of the shell halves and the mechanics involved when they come together. This ensures an almost perfect fit even when the shell is damaged and regrows. Edges in some species are wavy because the mantle grows faster than the shell edge, causing buckling. The interlocking pattern is constrained by the forces on the shells when closed.
|
|
Big whorls have little whorls
Which feed on their velocity, And little whorls have lesser whorls And so on to viscosity. Lewis Fry Richardson |
Jacob Bedrossian, Samuel Punshon-Smith, and Alex Blumenthal (U Maryland) find first rigorous proof of Batchelor's law, fundamental to turbulent fluid flow. This previously empirical law states that the power spectrum of small and large whorls in a turbulent fluid scales with wavenumber to the power -1. The proof was presented at a SIAM meeting in December 2019.
|
|
The Birch-Swinnerton-Dyer Conjecture about rational points on an elliptic curve is one of the major open problems in mathematics. It emerged from an early computer experiment. Now Laura Alessandretti, Andrea Baronchelli, and Yang-Hui He have employed state-of-the-art computing to gain new insights. Using the Cremona database they inspect over 2.5 million elliptic curves using machine-learning and topological data analysis, finding new patterns in elliptic curve data.
|
|
Over 40 years ago (exact date unknown) Paul Erdös conjectured that any subset A of the positive integers with positive density contains B+C where B and C are infinite subsets. Using methods from ergodic theory, Joel Moreira, Florian Karl Richter, and Donald Robertson have now proved the conjecture.
|
|
Mohammad Ghomi and Joel Spruck have proved that the total positive curvature of any closed hypersurface in a complete simply connected n-dimensional manifold of nonpositive curvature is bounded below by the volume of the unit sphere in n-dimensional Euclidean space. This yields the optimal isoperimetric inequality for bounded regions of finite perimeter, which proves the Cartan-Hadamard conjecture. The conjecture was proved for two dimensions in 1926, for four in 1984, and for three in 1992. The new work polishes off all other dimensions.
|
|
Take any integer n > 0. If n is even, divide by 2; if odd, replace by 3n+1. Repeat indefinitely. The Collatz (or 3n+1) Conjecture states that the process always reaches n = 1, and then cycles 1, 4, 2, 1, 4, 2, ... . This conjecture has many names, and has long resisted efforts at a proof or disproof. Now Terry Tao has made significant progress using techniques from probability theory. Roughly, he proves that almost all n (in the sense of logarithmic density) eventually attain a value much smaller than n (less than f(n) for any f such that f(n) tends to infinity with n, such as log log log log n). A complete proof remains out of reach by these methods.
|
|
42 is interesting after all...
|
Which numbers are sums of three (positive or negative) cubes? A team led by the University of Bristol and MIT has solved a famous maths puzzle with an answer for the most elusive number of all: 42. The problem, set in 1954, looked for Solutions of the Diophantine Equation x^3+y^3+z^3=k, with k being all the numbers from 1 to 100. Until recently only 33 and 42 held out. Then 33 was solved, and finally 42. The numbers are x = -80538738812075974, y = 80435758145817515, z = 12602123297335631.
|
|
Paul Krapivsky and Sidney Redner take a new look at an old optimisation problem to compare three strategies for parking your car. The "meek" strategy picks the first available. The "optimistic" strategy looks for a space next to the entrance, then backtracks to the closest vacancy. "Prudent" drivers drive past the first available space, betting that another space exists further in; then backtrack to the space a meek driver would have claimed initially if there isn't one. Which is best? There's also an unexpected connection to the microtubule "scaffolding" of living cells, which made it possible to find a solution.
|